Answer:
A) z = -0.05
B) z = 0.41
C) Amy
Explanation:
Remember that the formula we use to calculate a z-score is:
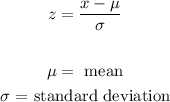
Let's calculate the z-score for Catherine's test grade:
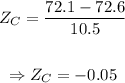
Now, let's calculate the z-score for Amy's test grade:
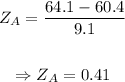
Since the z-score for Amy's test grade is greater than Catherine's, we can conclude that Amy perfomed better.