Question

Look at image, thus is a homework problem i need help with, thank you!

Answer 1

The given expression is:

`\sin (-t)-\sin t`

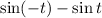
Recall the definition of an odd function:

`f(-x)=-f(x)`

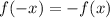
Since the sine function is an odd function, it follows that:

`\sin (-t)=-\sin t`

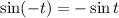
Substitute this into the given expression:

`\sin (-t)-\sin t=-\sin t-\sin t`

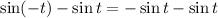
Simplify the expression:

`-2\sin t`

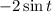
Substitute sin t =a into the expression:

`\begin{gathered} -2(a) \\ =-2a \end{gathered}`

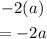
Hence, the expression in terms of a is -2a.

The answer is -2a.