Question

a planets circumference is approximately 39,750 km. with this circumference, what is it's radius? use this measurement to determine the length of an arc from the North Pole of the Equator.

Answer 1

a)

The rule of the circumference of the circle is

`C=2\pi\text{ r}`

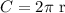
Where r is the radius of the circle

since the circumference of the circle is 39750, then

C = 39750

Substitute it in the rule to find r and use pi = 3.14

`\begin{gathered} 39750=2(3.14)(r) \\ 39750=6.28r \end{gathered}`

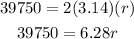
Divide both sides by 6.28

`\begin{gathered} (39750)/(6.28)=(6.28r)/(6.28) \\ 6329.617834=r \end{gathered}`

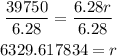
Round it to the nearest whole number

r = 6330 km

b)

Since the equator is at 0 degree

Since the North is at 90 degrees

Then the angle between them is 90 degrees

Since the measure of the circle is 360 degrees

Then the arc between the equator and the North is

`(90)/(360)=(1)/(4)`

Then the length of the arc between them is 1/4 C

Since C = 39750, then

Round it to the nearest whole number

L = 9938 km