Given:
The height (h) of the ball after t seconds is given by the relationship:
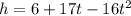
Solution
We are required to find the values of t for which the ball's height is 10 feet.
We set h = 10 feet and then solve the resulting equation.
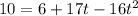
We can then solve the equation:
![\begin{gathered} -16t^2\text{ + 17t + 6 - 10 = 0} \\ -16t^2\text{ + 17t - 4 = 0} \\ \text{Divide through by -1} \\ 16t^2\text{ - 17t + 4 = 0} \\ U\sin g\text{ quadratic formular,} \\ x\text{ = }\frac{-b\text{ }\pm\sqrt[]{b^2-4ac}}{2a} \\ we\text{ have,} \\ t\text{ = 0.71s or 0.35s (nearest hundredth)} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/4bk6cak3yk62tto3q37j48vqzu30jbpnsd.png)
Answer: 0.71 sec or 0.35 sec