SOLUTION:
Case: Similar shapes (Area of Rectangles)
Given:
Similar triangles ABCD and WXYZ.
|XY| = 6 in
Area of WXYZ = 24 sq in
|AD| = 24 in
Required: To find the Area of ABCD
Method:
Step 1: We find the length of side WX
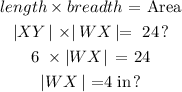
Step 2: Use similar sides to get the width |AB| of ABCD
Since the scale factor is 4 from WXYZ and ABCD
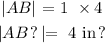
Step 3: Now we find the Area of ABCD
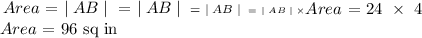
Final answer:
The area of ABCD is 96 sq in