Question

Determine whether the events described are overlapping or non-overlapping. Then find the either/or probability of the event.Randomly meeting a four-child family with either exactly one or exactly two boy children.

Answer 1

Step-by-step explanation: To solve this question we need to know some rules as follows

- overlapping events occur when both may happen at the same time

- non-overlapping events occur when they can not happen at the same time

- Once we have an either/or probability we use the sum of the probabilities to find the final probability.

Step 1: First we know that if we "randomly meet a four​-child family with either exactly one or exactly two boy children" we can see that there is no possibility to happen both events at the same time (if you have just 1 boy so you don`t have 2 boys) which means this is a non-overlapping event.

Step 2: Now let's focus on the possible events for a four​-child family once the possible outcomes are B = boy and G = girls as follows

BBBB. BBBG. BBGB. BGBB. GBBB. BBGG. BGBG. BGGB. GBGB. GGBB. GBBG. BGGG. GBGG. GGBG. GGGB. GGGG.

Step 3: As we can see there are 16 possible events and we have that

`\begin{gathered} P_(1boy)=(4)/(16) \\ and \\ P_(2boys)=(6)/(16) \end{gathered}`

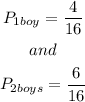
Step 4: Now we just need to calculate the either/or probability by adding the probabilities as follows

`\begin{gathered} P_(ether|or)=P_(1boy)+P_{2boys_{\placeholder{⬚}}} \\ P_(ether|or)=(4)/(16)+(6)/(16) \\ P_(ether|or)=0.625 \end{gathered}`

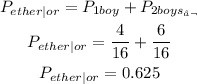
Final answer: So the final answers are Non-overlapping and P = 0.625