Question

If a || b, m<2=63°, and m<9=105°, find the missing measure of m<6=?

Answer 1

From the given graph, the following angle relationships are observed:

∠9 and ∠10 are Supplementary. This means that the sum of two angles is 180°.

∠10 and ∠6 are Corresponding Angles. This means that the two angles must be congruent.

For us to be able to find the measure of ∠6, we first determine the measure of ∠10.

Given:

∠9 = 105°

∠2 = 63°

Step 1: Determining the measure of ∠10.

`\text{ }\angle9\text{ + }\angle10=180^(\circ)`
`\text{ }105^(\circ)\text{+ }\angle10=180^(\circ)`
`\text{ }\angle10=180^(\circ)\text{ - }105^(\circ)`
`\text{ }\angle10=75^(\circ)`

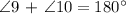
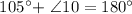
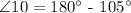
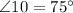
Step 2: Determine the measure of ∠6.

`\angle6\text{ = }\angle10\text{ ; Corresponding angle}`
`\angle6=75^(\circ)`

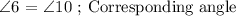
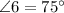
Therefore, the measure of ∠6 is 75°.