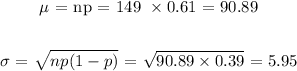Question

Consider the probability that no less than 94 out of 149 people have not been in a car accident. Assume the probability that a given person has not been in a car accident is 61%.Approximate the probability using the normal distribution. Round your answer to four decimal places.

Answer 1

Explanation:

Binomial probability distribution

Probability of exactly x successes on n repeated trials, with p probability.

Can be approximated to a normal distribution, using the expected value and the standard deviation.

The expected value of the binomial distribution is:

`E(x)\text{ = np}`

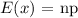
The standard deviation of the binomial distribution is:

`\sigma\text{ = }√(np(1-p))`

Normal probability distribution

Problems of normally distributed samples can be solved using the z-score formula.

In a set with mean and standard deviation , the zscore of a measure X is given by:

`z\text{ = }(x-\mu)/(\sigma)`

p = 61% = 0.61

n = 149

`\begin{gathered} \mu\text{ = np = 149 }*0.61\text{ = 90.89} \\ \\ \sigma\text{ = }√(np(1-p))\text{ = }√(90.89*0.39)\text{ = 5.95} \end{gathered}`
`\begin{gathered} z\text{ = }(x-\mu)/(\sigma)\text{ = }(94-90.89)/(5.95) \\ \\ z\text{ = 0.523} \end{gathered}`