First, we need to draw the points on the plane to get a better idea of the problem, as shown below
We can obtain the distance between the points and then use the next formula
![\begin{gathered} A=\sqrt[]{s(s-a)(s-b)(s-c)} \\ \text{where} \\ s=(a+b+c)/(2) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/2qb1juvxwkvzri21t7r3ert7xuelemtgmw.png)
where a, b and c are the sides of the triangle.
In our case,
![\begin{gathered} a=d(AB)=\sqrt[]{(-2-3)^2+(3-6)^2}=\sqrt[]{25+9}=\sqrt[]{34} \\ b=d(BC)=\sqrt[]{(3-2)^2+(6--2)^2}=\sqrt[]{1+64}=\sqrt[]{65} \\ c=d(CA)=\sqrt[]{(2--2)^2+(-2-3)^2}=\sqrt[]{16+25}=\sqrt[]{41} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/2xw398s302eyq014p9z7cmedfuvrvmepf1.png)
Then, the area is
![\begin{gathered} \Rightarrow s=\frac{\sqrt[]{34}+\sqrt[]{65}+\sqrt[]{41}}{2} \\ \Rightarrow A=\sqrt[]{\frac{\sqrt[]{34}+\sqrt[]{65}+\sqrt[]{41}}{2}(\frac{-\sqrt[]{34}+\sqrt[]{65}+\sqrt[]{41}}{2})(\frac{\sqrt[]{34}-\sqrt[]{65}+\sqrt[]{41}}{2})(\frac{\sqrt[]{34}+\sqrt[]{65}-\sqrt[]{41}}{2})} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/abjy0y9hry2qk1ekk2mo8hj2nbzgizhbnl.png)
Simplifying the expression,
![\Rightarrow A=\sqrt[]{((1)/(16))(72+2\sqrt[]{2665})(2\sqrt[]{2665}-72)}](https://img.qammunity.org/2023/formulas/mathematics/high-school/vxzoybf5nj1sbuwdgp4hznxiced8lt1cbn.png)
Therefore,
![\Rightarrow A=\sqrt[]{(1)/(16)(4\cdot2665-72^2)}=\sqrt[]{((1)/(16))5476}=\sqrt[]{342.25}](https://img.qammunity.org/2023/formulas/mathematics/high-school/dt9zoxu5526uqjlxormnhjoaqkakffrco5.png)
Finally,
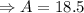
The area of the triangle is 18.5 square units, and the perimeter is
![P=\sqrt[]{34}+\sqrt[]{65}+\sqrt[]{41}=20.296333\ldots\approx20.3](https://img.qammunity.org/2023/formulas/mathematics/high-school/jqxdidbbjvm7jgsa8658kak5aoiqdt4di5.png)
The perimeter is 20.3 units