Question

Find the values of x and y when the smaller triangle has an area of 108 cm2.The value of x is cm and the value of y is cm.(Type exact answers, using radicals as needed. Rationalize all denominators.)

Answer 1

The two angles of the right angle triangles are equal. Hence both the triangles are similar.

From the property of simialr triangle the sides of the triangles are proportional,

`\begin{gathered} (72)/(x)=(81)/(y) \\ (y)/(x)=(81)/(72)=(9)/(8) \end{gathered}`

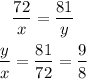
Let y=9k and x=8k.

The area of the smaller triangle is 108 square centimeter.

`\begin{gathered} A=108 \\ (1)/(2)xy=108 \\ (1)/(2)(9k)(8k)=108 \\ 36k^2=108 \\ k=\sqrt[]{3} \end{gathered}`

Thus, the requried value of x and y are,

`\begin{gathered} x=9\sqrt[]{3} \\ y=8\sqrt[]{3} \end{gathered}`

Thus, the above are the values of x and y.