Question

How many grams of silver chromate will precipitate when 250. mL of 0.450 M silver nitrate are added to 150. mL of 0.500 M potassium chromate? 2 AgNO3(aq) + K2CrO4(aq) Ag2CrO4(s) + 2 KNO3(aq)

Answer 1

They give us the balanced equation of the reaction, so we can continue with the calculations. To find the moles of Silver Chromate (Ag2CrO4) we will follow the following steps:

1) We find the moles of reactants that we have, clearing the moles of the molarity equation. Molarity refers to moles of solute per volume of solution.

`Molarity=(MolesSolute)/(Lsolution)`

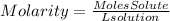
2) We find the limiting reagent by comparing the theoretical AgNO3 to K2CrO4 ratio with the actual one. The theoretical ratio AgNO3 to K2CrO4 is 2/1. If the ratio we find is less than 2, the limiting reagent will be AgNO3. But, if the ratio is greater than 2, the limiting reagent will be K2CrO4.

3) By stoichiometry we find the moles of Ag2CrO4 that are formed using the moles of the limiting reactant.

4) We calculate the grams of Ag2CrO4 by multiplying the moles found by its molar mass. Molar mass Ag2CrO4: 331.73g/mol

Let's proceed with the calculation:

1)Moles of reactants

Moles of AgNO3

`\begin{gathered} MolesSolute=Molarity* Lsolution \\ MolesSolute=0.450M*0.250L=0.113molAgNO_3 \end{gathered}`

Moles of K2CrO4

`\begin{gathered} MolesSolute=Molar\imaginaryI ty* Lsolut\imaginaryI on \\ MolesSolute=0.500M*0.150L=0.0750molK_2CrO_4 \end{gathered}`

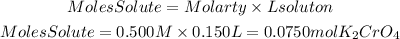
2) Limiting reactant

We have that the actual ratio AgNO3 to K2CrO4 is:

`(AgNO3)/(K_2CrO_4):1.5`

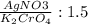
The actual ratio is less than the theoretical one, which is 2/1. So the limiting reactant is Ag2CrO4

3) Moles of Ag2CrO4

We have that the ratio Ag2CrO4 to AgNO3 is 1/2, so the moles that will be formed of Ag2CrO4 will be:

`\begin{gathered} MolAg_2CrO_4=GivenmolAgNO3*(1molAg_2CrO_4)/(2molAgNO_3) \\ MolAg_2CrO_4=0.113AgNO3*(1molAg_2CrO_4)/(2molAgNO_3)=0.0563molAg_2CrO_4 \end{gathered}`

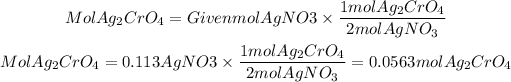
4)Grams of Ag2CrO4

`\begin{gathered} gAg2CrO4=GivenmolAg2CrO4*(MolarMass,gAg2CrO4)/(1molAg2CrO4) \\ gAg2CrO4=0.0563molAg2CrO4*(331.73gAg2CrO4)/(1molAg2CrO4)=18.6gAg2CrO4 \end{gathered}`

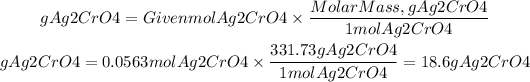
Answer: It will be precipitated 18.6grams of silver chromate (Ag2CrO4)