Question

For #1 solve for x. then find the missing piece(s) of the parallelogram.

Answer 1

• x=10

,

• Given side lengths: 41 units

Explanation:

In a parallelogram, opposite side lengths are equal. Therefore, from the given figure:

`5x-9=3x+11`

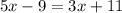
The equation is then solved for x:

`\begin{gathered} 5x-9=3x+11 \\ \text{Subtract 3x from both sides} \\ 5x-3x-9=3x-3x+11 \\ 2x-9=11 \\ \text{Add 9 to both sides of the equation} \\ 2x-9+9=11+9 \\ 2x=20 \\ \text{ Divide both sides of the equation by 2} \\ (2x)/(2)=(20)/(2) \\ x=10 \end{gathered}`

The value of x is 10.

Next, the length of the given sides is found.

`\begin{gathered} 3x+11=3(10)+11 \\ =30+11 \\ =41\text{ units} \end{gathered}`

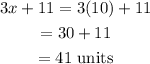
The length of the given parallel sides is 41 units.