Question

2) A line passes through the points (5,-1) and (8,3). This line also passes through thepoint (17,k). Find the value of k. Show your work.

Answer 1

The line is passing through the points (5,-1) and (8,3).

Thus, we form the equation of the line with these two coordinates

and to find the value of k, from(17,k)

as the line also passes through the point (17, k), So, the point (17, k) must satisfy the equation of line.

The general equation of line :

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

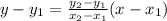
Substitute the coordinates : (5,-1) and (8,3).

`\begin{gathered} y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1) \\ y-(-1)=(3-(-1))/(8-5)(x-5) \\ y+1=(3+1)/(3)(x-5) \\ y+1=(4)/(3)(x-5) \\ y=(4)/(3)(x-5)-1 \end{gathered}`

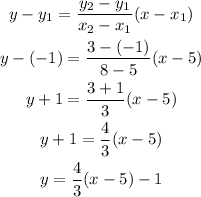
The equation of line : y = 4/3(x - 5) - 1

As the point ( 17, k) is also passes through the same line, so they must satisfy the equation of line.

`\begin{gathered} y=(4)/(3)(x-5)-1 \\ k=(4)/(3)(17-5)-1 \\ k=(4)/(3)(12)-1 \\ k=(4*12)/(3)-1 \\ k=(4*4)/(1)-1 \\ k=16-1 \\ k=15 \\ \end{gathered}`

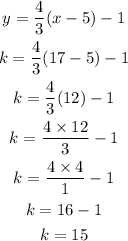
k = 15

Answer : k = 15