Given data
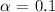
Given claim: proportional difference from 57%
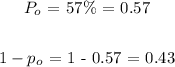
Thus,
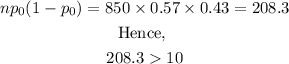
The sample size n is the number of parents surveyed from the entire population
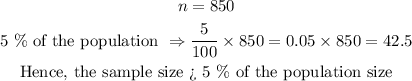
Since the sample size is greater than 5% of the population, it can be reasonably assumed to be random.
The requirements for testing the hypothesis are satisfied.