Question

Select the correct answer.If f(x) = 2x2 - X-6 and g(x) = x2 - 4, find f(x) = g(x).A.21 + 3I - 2B.21 - 3I + 2C.21 + 3I + 2OD. ?21 - 3I - 2

Answer 1

The functions we have are:

`\begin{gathered} f(x)=2^{}x^2-x-6 \\ g(x)=x^2-4 \end{gathered}`

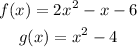
The division of the functions is:

`(f(x))/(g(x))=(2x^2-x-6)/(x^2-4)`

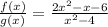
We need to factor both the numerator f(x) and the denominator g(x) to find our answer.

Factoring 2x^2-x-6:

`2x^2-x-6=(2x+3)(x-2)`

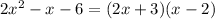
Factoring x^2-4:

`x^2-4=(x+2)(x-2)`

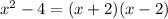
And we substitute this in the division:

`(f(x))/(g(x))=((2x+3)(x-2))/((x+2)(x-2))`

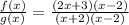
x-2 in the numerator and denominator cancel each other, and the final result is:

`(f(x))/(g(x))=(2x+3)/(x+2)`

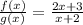
Option C