Question

(e) 4x2 + y2 = 64 Graph the vertices, foci, endpoints of the minor axis, and endpoints of the latera recta; then draw 2. the ellipse for each equation in problem 1. AB is a chord of the partial ellipse with equation f() = a - *. Find the length of AB using (a) 576x2 + 62 5y2 = 360,000, A(15,f(15)), B(20,f(20)) (b) 49x2 + 625y2 = 30,625, A(15,f(15)), B(20,f(20)) try test on each of the following ellipses. (c) x² + 46. 4y2 = 36 (6) 25x' + 16y? - 400 (d) 4x2 + y2 = 4 () x2 + 4y2 = 36 (h) 7x2 + 8y = 112 (g) 9x2 + ketch: then find the equation of

Answer 1

we have the equation

`576x^2+625y^2=360,000`

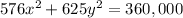
Simplify

Divide both sides by 360,000

so

`\begin{gathered} (576)/(360,000)x^2+(625)/(360,000)y^2=(360,000)/(360,000) \\ \\ \\ (x^2)/(625)+(y^2)/(576)=1 \end{gathered}`

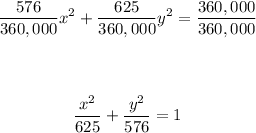
Remember that

625=25^2

576=24^2

substitute

`(x^2)/(25^2)+(y^2)/(24^2)=1`

so

a^2=25 and b^2=24

we have the function f(x)

`f(x)=(b)/(a)\sqrt[]{a^2-x^2}`

the point A is (15,f(15))

Calculate f(15)

`f(15)=\frac{\sqrt[]{24}}{\sqrt[]{25}}\sqrt[]{25^2-15^2}`
`f(15)=\frac{2\sqrt[]{6}}{5}\sqrt[]{400}`

simplify

`f(15)=8\sqrt[]{6}`

the point A is

`A(15,\text{ 8}\sqrt[]{6})`

Find the point B

B(20,f(20)

Calculate f(20)

`f(20)=\frac{\sqrt[]{24}}{\sqrt[]{25}}\sqrt[]{25^2-20^2}`
`f(20)=6\sqrt[]{6}`

the point B is

`B(20,6\sqrt[]{6})`

Determine the distance between A and B

Applying the formula to calculate the distance between two points

`d=\sqrt[\square]{(y2-y1)^2+(x2-x1)^2}`

substitute the given values of A and B

`d_(AB)=\sqrt[\square]{(6\sqrt[]{6}-8\sqrt[]{6})^2+(20-15)^2}`
`\begin{gathered} d_(AB)=\sqrt[\square]{24+25} \\ d_(AB)=7 \end{gathered}`

therefore

the length of AB is 7 units