Question

A technical machinist is asked to build a cubical steel tank that will hold 180 L of water.Calculate in meters the smallest possible inside length of the tank. Round your answer to the nearest 0.001 m.

Answer 1

The smalles possible inside length will be the one that gives exactly the volume needed, anything less won't hold the required volume of water.

Since it is cubical, all sides have the same length and the volume will be:

`V=l^3`

Let's first convert L to m³. 1 L is equivalent to 0.001 m³, so 180 L is equivalent to

`180\cdot0.001=0.18m^3`

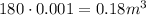
Now, we input that volume into the fisrt equation and solve for "l":

`\begin{gathered} 0.18=l^3 \\ l=\sqrt[3]{0.18}=0.56462\ldots\approx0.565 \end{gathered}`

So, the smallest possible inside length of the tank is approximately 0.565 m.