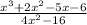Happy New Year’s thank you for helping see attached photo to understand problem

Question

asked Apr 9, 2023 28.6k views

1 Answer

Radim · Answer 1 · 2023-04-15T09:23:22+0000

We must compute and simplify the following expression:

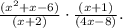
$((x^2+x-6))/((x+2))\cdot(\mleft(x+1\mright))/(\mleft(4x-8\mright))\text{.}$

This expression can be rewritten in the following way:

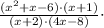
$((x^2+x-6)\cdot\mleft(x+1\mright))/((x+2)\cdot\mleft(4x-8\mright))\cdot$

1) Applying the distributive property for the product in the numerator, we have:

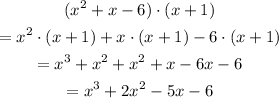
$\begin{gathered} (x^2+x-6)\cdot(x+1) \\ =x^2\cdot(x+1)+x\cdot(x+1)-6\cdot(x+1) \\ =x^3+x^2+x^2+x-6x-6 \\ =x^3+2x^2-5x-6 \end{gathered}$

2) Doing the same for the product in the denominator, we get:

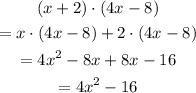
$\begin{gathered} (x+2)\cdot(4x-8) \\ =x\cdot(4x-8)+2\cdot(4x-8) \\ =4x^2-8x+8x-16 \\ =4x^2-16 \end{gathered}$

Using the previous results for the numerator and denominator, the original expression is rewritten as:

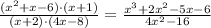
$((x^2+x-6)\cdot(x+1))/((x+2)\cdot(4x-8))=(x^3+2x^2-5x-6)/(4x^2-16)$

Answer