Question

Miguel drove to the mountains last weekend. There was heavy traffic on the way there, and the trip took 8 hours. When Miguel drove home, there was no traffic and the trip only took 6 hours. If his average rate was 16 miles per hour faster on the trip home, how far away does Miguel live from the mountains? Do not do rounding .

Answer 1

Let, the rate of the speed be r.

The distance is given by,

`\text{distance = rate}*\text{ time}`

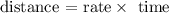
The trip took 8 hours and the distance traveled in 8 hours is,

`D=8r\ldots\ldots\ldots\ldots(1)`

While retuening , there was no traffic and trip takes 6 hours and average rate is 16 mph faster.

the distance is,

`D=6(r+16)\ldots\ldots\ldots\ldots\ldots(2)`

Equating both the questions,

`\begin{gathered} 8r=6(r+16) \\ 8r-6r=80 \\ 2r=80 \\ r=40\text{mph} \end{gathered}`

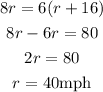
Distance is,

`\begin{gathered} D=8r \\ D=8*(80)/(3) \\ D=213.3333\text{ miles} \end{gathered}`

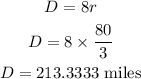
Answer:

Rate is 80/3 mph

distance is 213.3333 miles.