Question

Lucy the trainer has two solo workout plans that she offers her clients: Plan A and Plan B. Each client does either one or the other (not both). On Friday therewere 5 clients who did Plan A and 3 who did Plan B. On Saturday there were 2 clients who did Plan A and 6 who did Plan B. Lucy trained her Friday clients for atotal of 10 hours and her Saturday clients for a total of 10 hours. How long does each of the workout plans last?Х$?Length of each Plan A workout: hour(s)Length of each Plan B workout: 1 hour(s)

Answer 1

Length of Plan A workout: 1.25 hours

Length of Plan B workout: 1.25 hours

Step-by-step explanation:

Let x represent the length of Plan A workout

Let y represent the length of Plan B workout

In the question, we're told that, on Friday, there were 5 clients who did Plan A and 3 who did Plan B, and Lucy trained them for a total of 10 hours. We can express this mathematically as;

`5x+3y=10\ldots\ldots\text{.Equation 1}`

We're also told that, on Saturday, there were 2 clients who did Plan A and 6 who did Plan B, and Lucy trained them for a total of 10 hours. We can also express this mathematically as;

`2x+6y=10\ldots\ldots\ldots\text{.Equation 2}`

We'll now solve both equations simultaneously following the below steps;

Step 1: Multiply Equation 1 by 2;

`\begin{gathered} 2*(5x+3y)=10*2_{} \\ 10x+6y=20\ldots\ldots\text{.}\mathrm{}\text{Equation 3} \end{gathered}`

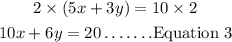
Step 2: Subtract Equation 2 from Equation 3 and solve for x;

`\begin{gathered} 8x=10 \\ x=(10)/(8) \\ x=(5)/(4) \\ x=1.25\text{hours} \end{gathered}`

Step 3: Substitute x with 5/4 in Equation 1 and solve for y;

`\begin{gathered} 5x+3y=10 \\ 3y=10-5x \\ 3y=10-5((5)/(4)) \\ 3y=(40-25)/(4) \\ 3y=(15)/(4) \\ y=(15)/(12) \\ y=(5)/(4) \\ y=1.25\text{ hours} \end{gathered}`

We can see from the above that the length of Plan A workout is 1.25 hours and the length of Plan B workout is also 1.25 hours