Question

What are the dimensions of the fenced in area if he only has 190 yards and the length is 10 yards more than 8 times the width

Answer 1

Considering the fenced area is a rectangular area, the total fencing is represented by the perimeter of the area, that is:

`\text{perimeter}=2\cdot\text{length}+2\cdot\text{width}`

If the total fencing is 190 yards, we have:

`\begin{gathered} 2\cdot\text{length}+2\cdot\text{width}=190 \\ \text{length}+\text{width}=95 \end{gathered}`

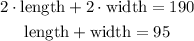
The length is 10 yards more than 8 times the width, so we have:

`\text{length}=10+8\cdot\text{width}`

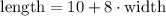
Using this value of the length in the first equation, we have that:

`\begin{gathered} (10+8\cdot\text{width)}+\text{width}=95 \\ 10+9\cdot\text{width}=95 \\ 9\cdot\text{width}=85 \\ \text{width}=(85)/(9)=9.44 \end{gathered}`

Now, finding the value of the length, we have:

`\begin{gathered} \text{length}=10+8\cdot\text{width} \\ \text{length}=10+8\cdot(85)/(9) \\ \text{length}=10+(680)/(9) \\ \text{length}=(90)/(9)+(680)/(9)=(770)/(9)=85.56 \end{gathered}`

So the dimensions of the fencing are length = 85.56 and width = 9.44.