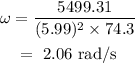Question

Two astronauts, each having a mass of 74.3 kg are connected by a 13.1 m rope of negligible mass. They are isolated in space, orbiting their center of mass at speeds of 5.65 m/s.a. Calculate the magnitude of the initial angular momentum of the system by treating the astronauts as particlespart b) is Calculate the rotational energy of the system. and part c)By pulling the rope, the astronauts shorten the distance between them to 5.99 m. What is the new angular velocity of the astronauts?

Answer 1

Given that the mass of each astronaut is m = 74.3 kg

The distance between the two astronauts is d = 13.1 m

The speed of the astronaut is v = 5.65 m/s.

(a) We have to find the angular momentum.

The formula to find angular momentum is

`\begin{gathered} L\text{ = (}(1)/(2)d)mv+\text{(}(1)/(2)d)mv \\ =\text{dmv} \end{gathered}`

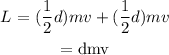
Substituting the values, the angular momentum will be

`\begin{gathered} L=74.3*13.1*5.65 \\ =5499.31kgm^2\text{/s} \end{gathered}`

(b) We have to find the rotational energy.

The rotational energy can be calculated by the formula

`\begin{gathered} E=(L^2)/(2((2md)/(2))) \\ =(L^2)/(2md) \end{gathered}`

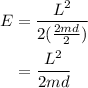
Substituting the values, the rotational energy will be

`\begin{gathered} E=((5499.31)^2)/(2*74.3*13.1) \\ =1.554*10^4\text{ J} \end{gathered}`

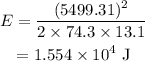
(c) We have to find the angular velocity when d'= 5.99 m

The formula to find the new angular velocity is

`\omega=(L)/(d^(\prime2)m)`

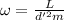
Substituting the values, the angular velocity will be

`\begin{gathered} \omega=(5499.31)/((5.99)^2*74.3) \\ =\text{ 2.06 rad/s} \end{gathered}`