Question

Determine whether A ABC is similar to ADEF. If so state how do you know. (G.SRT.A3)

Answer 1

Given the triangles ΔABC and ΔDEF, if these triangles are similar, then the corresponding sides should be at the same ratio and the corresponding angles should be congruent.

We don't know the measures of the sides of the triangles, so we cannot prove if they are or are not at the same ratio but we know two of the inner angles. This means that to prove similarity between the triangles we have to compare the corresponding angles.

To determine which angles are corresponding, you have to take a look at the way the triangles are named, the order of the letters indicates the corresponding vertices:

The pair of corresponding angles ∠A and ∠D is congruent since both angles measure 104º

To determine if the other corresponding angles are congruent, first, you have to calculate the measure of the missing angles ∠C and ∠E, to do so you have to remember that the sum of the inner angles of a triangle is equal to 180º.

∠C

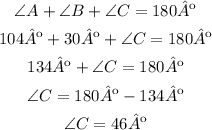
`\begin{gathered} \angle A+\angle B+\angle C=180º \\ 104º+30º+\angle C=180º \\ 134º+\angle C=180º \\ \angle C=180º-134º \\ \angle C=46º \end{gathered}`

∠E

`\begin{gathered} \angle D+\angle E+\angle F=180º \\ 104º+\angle E+46º=180º \\ \angle E+150º=180º \\ \angle E=180º-150º \\ \angle E=30º \end{gathered}`

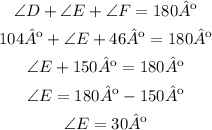
The corresponding angles ∠B and ∠E measure 30º, and the corresponding angles ∠C and ∠F measure 46º.

Since all corresponding angles are congruent you can say that these triangles are similar by AA.

The correct option is A