Question

I understand the first part of problem 13 but I don’t know how to do the next parts

Answer 1

B)

Given:

The coordinates of line segment XY is, X (-2,1) and Y (3,6).

The objective is to determine the equation of perpendicular bisector of line segment XY.

Step-by-step explanation:

The equation of perpendicular bisector can be calculated by finding the slope of line segment XY and its midpoint.

Consider the coordinates of XY as,

`\begin{gathered} (x_1,y_1)=(-2,1) \\ (x_2,y_2)=(3,6) \end{gathered}`

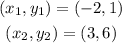
The slope of XY can be calculated as,

`\begin{gathered} m_1=\frac{y_2-y_1}{x_2-x_1_{}} \\ =(6-1)/(3-(-2)) \\ =(5)/(5) \\ =1 \end{gathered}`

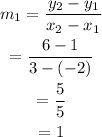
To find midpoint of line 1:

Now the midpoint of the line segment XY can be calculated as,

`\begin{gathered} M_1=((x_1+x_2)/(2),(y_1+y_2)/(2)) \\ =((-2+3)/(2),(1+6)/(2))_{} \\ =((1)/(2),(7)/(2)) \end{gathered}`

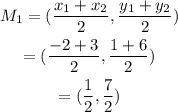
To find slope of line 2:

Since, the second line is perpendicular to line 1, slope of line 2 can be calculated as,

`\begin{gathered} m_1* m_2=-1_{} \\ m_2=-(1)/(m_1) \\ =-(1)/(1) \\ =-1 \end{gathered}`

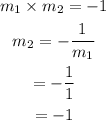
To find equation of line 2:

Now, the equation of second line can be calculated using the slope and point formula.

`\begin{gathered} y-y_1=m(x-x_1) \\ y-(7)/(2)=-1(x-(1)/(2)) \\ y-(7)/(2)=-x+(1)/(2) \\ y=-x+(1)/(2)+(7)/(2) \\ y=-x+(8)/(2) \\ y=-x+4 \end{gathered}`

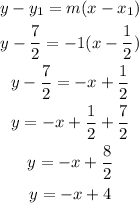
Hence, the equation of perpendicular bisector of line segment XY is

y = -x + 4.