It was given that the length of stretch is directly proportional to the weight. Assuming the length is represented by l and the weight by w, we have the following relationship:
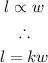
where k is a constant.
The question gives the following parameters:
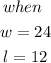
Therefore, we can calculate the constant to be:
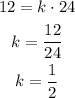
Therefore, the relationship will be:
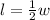
If the weight is increased to 43 pounds, the length will be:
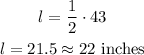
The spring will stretch 22 inches.