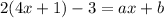
To find the solution of this equation you solve for x, you leave the terms with x in one side of the equation:
a. Remove the parenthesis: multiply 2 by the two terms in the parenthesis:

b. Leave in one side all the terms with x:
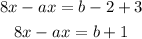
Then, for the given statements:
1. If a =8 and b= 1
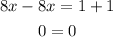
Then, the whit those values for a and b the equation has as solution all the real numbers, because 0=0.
Statement: False
2. If a = 4 and b = -2
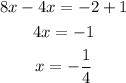
Then, the whit those values for a and b the equation has exactly one solution x= -1/4
Statement: False
3. If a = 8 and b = -1
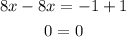
Then, the whit those values for a and b the equation has as solution all the real numbers, because 0=0.
Statement: False
4. If a = 2 and b = -1
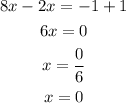
Then, the whit those values for a and b the equation has exactly one solution x=0
Statement: True
5. If a = 2 and b = 4
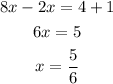
Then, the whit those values for a and b the equation has exactly one solution x=5/6
Statement: False