Question

I need someone to explain this to me I forgot how I solved it last time

Answer 1

Step-by-step explanation

We can rewrite the left side of the equation as follows:

`a\cdot a+b\cdot b\text{.}`

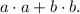
Now, multiplication and addition between rational numbers give always a rational number; then the number above is a rational number; let's denote it by d.

Thus (the square of c is a rational number, d)

`\begin{gathered} c^2=d, \\ c=\sqrt[]{d}\text{.} \end{gathered}`

But the square root of a rational number is not always a rational number. For example, the root of 2 is irrational!