Given data
(14)
*The given constant velocity of the plane take off is v = 175 km/ h = 48.61 m/s
*The given angle is
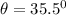
*The given time is t = 48.0 s
The vertical component of the velocity is calculated as
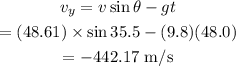
The horizontal component of the velocity is calculated as
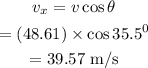
The formula for the velocity of the plane is given as
![v=\sqrt[]{(v_x_{})^2+(v_y)^2_{}}](https://img.qammunity.org/2023/formulas/physics/college/psyjt2s0rx522owf9e0w8mx495u3xnoohw.png)
Substitute the known values in the above expression as
![\begin{gathered} v=\sqrt[]{(39.57)^2+(-442.17)^2} \\ =443.93\text{ m/s} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/ww9q73d6oogqxqdn8nccaxfgqstodq6kwx.png)
Hence, the velocity of the plane in meter per second (m/s) is v = 443.93 m/s