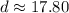Question

Find the distance between:(-6, -1) and(8, 10)Round your answer to the nearest hundredth.

Answer 1

The formula for calculate the distance between two points is the one shown below:

`d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}`

In this case, given the following points:

`\begin{gathered} \mleft(-6,-1\mright) \\ \mleft(8,10\mright) \end{gathered}`

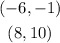
You can set up that:

`\begin{gathered} x_2=-6 \\ x_1=8 \\ y_2=-1 \\ y_1=10 \end{gathered}`

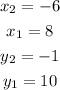
Now you can substitute values into the formula:

`d=\sqrt[]{(-6-8)^2+(-1-10)^2}`

Finally, evaluating and rounding to the nearest hundredth, you get:

`\begin{gathered} d=\sqrt[]{317} \\ d\approx17.80 \end{gathered}`

The answer is:

`d\approx17.80`