ANSWER
0.9738 or 97.38%
Step-by-step explanation
Given:
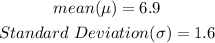
Desired Outcome:
Probability that it will last 10 years
z-score for the sample:

p-value
For the z-score of 1.9376, the p-value is 0.9738 or 97.38%
Hence, the probability that it will last longer than 10 years if you randonly purchase one item is 97.38%