Question

A flagpole has two wires attached to it, one of each side, that are tethered to the ground. Wire 1 makes a 41 degree angle with the ground, and is attached to a point 34 feet from the base of the pole. Wire 2 makes a 38 degree angle with the pole. A: How tall is the pole? B: How far from the base of the pole does wire 2 attach to the ground?. C: How long is wire 1?

Answer 1

In the diagram above we can see that we are asked to determine the value of "h", that is the height of the pole. To do that we will use the function tangent which is defined as:

`\tan \theta=\frac{opposite}{\text{adjacent}}`

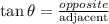
Replacing the values:

`\tan 41=(h)/(34)`

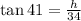
Solving for "h" we get:

`34\tan 41=h`

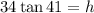
Solving the operations we get:

`29.6=h`

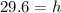
Therefore, the height of the pole is 29.6 feet.

Now we are asked to determine the distance from the base of wire 2. To do that we will use the function tangent for wire 2:

`\tan 38=(h)/(b)`

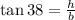
Now we solve for "b" first by multiplying both sides by "b":

`b\tan 38=h`

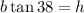
Now we divide both sides by tan38:

`b=(h)/(\tan 38)`

Replacing the value of "h":

`b=(29.6)/(\tan 38)`

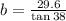
Solving the operations:

`b=37.9`

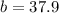
Therefore, the distance from the base of wire 2 is 37.9 feet.

Now we are asked to determine the longitude "L" of wire 1, to do that we will use the function cosine, which is defined as:

`\cos \theta=(adjacent)/(hypotenuse)`

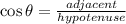
Replacing the values:

`\cos 41=(34)/(L)`

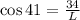
Now we solve for "L", first by multiplying by "L":

`L\cos 41=34`

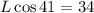
Now we divide both sides by cos41:

`L=(34)/(\cos 41)`

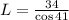
Solving the operations:

`L=45.1`

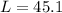
Therefore, the longitude of wire 1 is 45.1 feet.