Question

The problem is in the pictureI just need the h-1(7)

Answer 1

6

Step-by-step explanation

The inverse of a function will reverse the output and the input. To find the inverse of a function using algebra (if the inverse exists), set the function equal to y. Then, swap x and y and solve for y in terms of x. in other words ( x an y change position)

so

for (7)

`\begin{gathered} h(7)=6 \\ the\text{ coordinate is (7,6)} \end{gathered}`

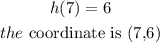
so, for h(x), when evaluating at (7) we got 6

hence, for the inverse it must happen the same, but y is the image, so

`\begin{gathered} h^(-1)=\mleft\{\mleft(8,5\mright),-7,7,-9,6,\mleft(7,6\mright)\mright\} \\ h^(-1)\mleft(7\mright)=6 \end{gathered}`

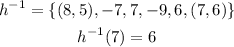
so, the answer is 6

I hope this helps you