SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Write the formula for calculating the area of the trapezoid
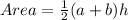
STEP 2: Write the given sides
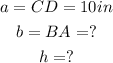
STEP 3: find the side AB
To get x from the included right-angled triangle, we use the cosine function as seen below:

Therefore, the value of:
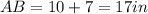
STEP 4: Find the height of the trapezoid
Using Pythagoras theorem,
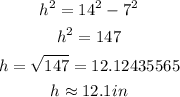
The height is approximately 12.1 inches
STEP 5: Find the area
By substitution,
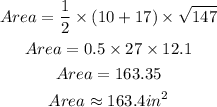
Hence, the area of the trapezoid is approximately 163.4in²