Question

A car starts from rest at a stop sign. It accelerates at 4.0 m/s^2 for 6 s, coasts for 2.0 s, and then slows down at a rate of 3.0 m/s^2 for the next stop sign How far apart are the stop signs?

Answer 1

The motion of the car between the first and last stops is divided in three parts:

• The motion where the car speeds up with acceleration of 4m/s^2.

,

• The motion without acceleration (when the car coasts for 2 seconds).

,

• The motion where the car slows down with acceleration of 3 m/s^2.

To determine how far apart the stop signs are we need to calculate how much distance the car traveled in each part. Let's analyze each situation.

First part of the motion.

For this part of the motion of the car we have a constant acceleration, this means that we have an uniform accelerated motion. To determine the distance traveled in this part we can use the equation:

`x=x_0+v_0t+(1)/(2)at^2`

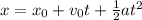
where x is the final position, x0 is the initial position, v0 is the initial velocity, a is the acceleration and t is the time.

In this case the initial position is zero (in here we are putting the origin of the motion at the stop sign), the initial velocity is zero (since the car starts from rest), the acceleration is 4 m/s^2 and the time is 6 seconds; plugging this values in the equation above we have that:

`\begin{gathered} x=0+0(6)+(1)/(2)(4)(6)^2 \\ x=(2)(36) \\ x=72 \end{gathered}`

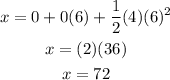
Hence, in this part of the motion the car travelled 72 meters.

We will need the final velocity for this part of the motion in order to calculate the distance traveled in the second part of the motion so let's calculate it. The final velocity can be obtained from the equation:

`a=(v_f-v_0)/(t)`

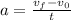
plugging the values we know and solving for the final velocity we have that:

`\begin{gathered} 4=(v_f-0)/(6) \\ v_f=(6)(4) \\ v_f=24 \end{gathered}`

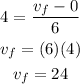
Therefore the car is traveling at 24 m/s when it starts to coast.

Second part of the motion.

In this part of the motion the car coasts, this means that it is not accelerating, and for this reason, the car does not change its velocity. For this reason we have an uniform rectilinear motion. The change in position in a rectilinear motion is given by:

`x=x_0+vt`

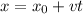
Changing our origin of the motion to where the car starts to coast we have that the initial position is zero, the velocity is 24 m/s (the velocity in which the car stopped accelerating) and the time is 2 seconds. Plugging this values in the equation we have that:

`\begin{gathered} x=0+(24)(2) \\ x=48 \end{gathered}`

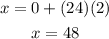
And then, we conclude, the car travelled 48 meters in this part of the motion.

Third part of the motion.

In here we know that the car is slowing down with an acceleration of 3 m/s^2 until it stops in the next stop sign. Since the acceleration is constant once again we have an uniform accelerated motion. To determine the distance the car traveled in this part we can use the equation:

`v^2_f-v^2_0=2a(x-x_0)`

In this case we know that the final velocity is zero (since the car stops), the initial velocity is 24 m/s (since the car was moving in an uniform rectiliniar motion in the previous part of the motion) and that the acceleration is -3 m/s^2 (we have to use a negative sign since the car is slowing down, this means that the acceleration is negative); plugging the values we have that:

`\begin{gathered} 0^2-24^2=2(-3)(x-0) \\ -576=-6x \\ x=(-576)/(-6) \\ x=96 \end{gathered}`

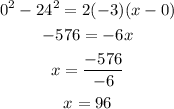
Hence in this part in the motion the car travelled 96 meters.

Finally, now that we know how much the car travelled in each part of the motion, we can calculate how far apart the stop signs are; to do this we add the distance the car travelled in each part, then we have:

`72+48+96=216`

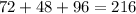
Therefore, the stops signs are 216 meters apart.