Given:
distance between Foci = 6 meters
Minor axis = 8 meters
Since distance is 6, f = 3
Minor axis is 8, b = 4
Let's use the Foci formula:
![f\text{ = }\sqrt[]{a^2-b^2}](https://img.qammunity.org/2023/formulas/mathematics/college/5a6rdl03dkhlle54n2dih1atabxafdff8n.png)
Solve for a:
![\begin{gathered} 3\text{ = }\sqrt[]{a^2-4^2} \\ \\ 3^2=(\sqrt[]{a^2-4^2})^2 \\ \\ 9=a^2-16 \\ \\ 9+16=a^2 \\ \\ 25=a^2 \\ \\ \sqrt[]{25}=a \\ \\ a\text{ = 5} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/vvhn8mbv3pyjrzhfxoabvu9405qoh4netb.png)
The equation will be:
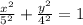
The length of the room is.
We have the vertices as:
Vertex, 1: (5, 0)
Vertex 2: (-5, 0)
The Length of the room = 5 + 5 = 10 meters
ANSWER:
Equation:
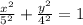
Length = 10 meters