Question

I attached a picture of the practice problem I'm trying to solve

Answer 1

Step-by-step explanation

From the statement, we know that:

`\begin{gathered} f(2)=0,\text{ }g(2)=-1, \\ \lim_(x\to2)\text{ }\lbrack f(x)+g(x)\rbrack=7, \\ \lim_(x\to2)\text{ }\lbrack2f(x)-g(x)\rbrack=-1. \end{gathered}`

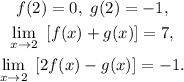
(a) Summing the given limits, applying the distributive property for the limit, we get:

`\begin{gathered} \lim_(x\to2)\text{ }\lbrack f(x)+g(x)\rbrack+\lim_(x\to2)\text{ }\lbrack2f(x)-g(x)\rbrack=7-1, \\ 3\lim_(x\to2)f(x)=6,\text{ } \\ \lim_(x\to2)f(x)=(6)/(3)=2. \end{gathered}`

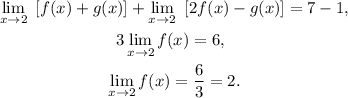
Using this result in the first given limit, we get:

`\begin{gathered} \lim_(x\to2)\lbrack f(x)+g(x)]=7, \\ \lim_(x\to2)f(x)+\lim_(x\to2)g(x)=7, \\ 2+\lim_(x\to2)g(x)=7, \\ \lim_(x\to2)g(x)=7-2=5. \end{gathered}`

(b) Putting the limit inside the square root and in the denominator, and then using the results from above, we get:

`\begin{gathered} \lim_(x\to2)\lbrack(√(g(x)+4))/(f(x))] \\ =(\lim_(x\to2)\lbrack√(g(x)+4)])/(\lim_(x\to2)f(x)) \\ =\frac{\sqrt{\lim_(x\to2)g(x)+4}}{\lim_(x\to2)f(x)} \\ =(√(5+4))/(2) \\ =(3)/(2). \end{gathered}`

(c) Putting the limit inside the exponent of the e power, and using the results from above, we get:

`\lim_(x\to2)\lbrack e^(f(x)-11)\rbrack=e^{\lim_(x\to2)f(x)-11}=e^(2-11)=e^(-9).`

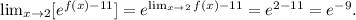
(d) Using the results from above, we get:

`\begin{gathered} \lim_(x\to2)\lbrack(f(x))^3-2g(x)+22] \\ =(\lim_(x\to2)f(x))^3-2\lim_(x\to2)g(x)+\lim_(x\to2)22 \\ =2^3-2\cdot5+22 \\ =20. \end{gathered}`Answer

a. 5

b. 3/2

c. e^(-9)

d. 20