Question

(x+1) and (x-4) are factors of x^3 + ax² + bx + c. The remainder is 6 when the cubic is divided by (x+2).Find the values of a, b and c.

Answer 1

Since (x + 1), (x - 4) are factors of

`x^3+ax^2+bx+c`

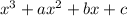
That means if x = -1 make the polynomial equal to 0, and x = 4 also make it = 0

Then we can make 2 equations from these informations

`\begin{gathered} x=-1 \\ (-1)^3+a(-1)^2+b(-1)+c=0 \\ -1+a-b+c=0 \\ a-b+c=1\rightarrow(1) \end{gathered}`
`\begin{gathered} x=4 \\ (4)^3+a(4)^2+b(4)+c=0 \\ 64+16a+4b+c=0 \\ 16a+4b+c=-64\rightarrow(2) \end{gathered}`

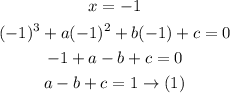
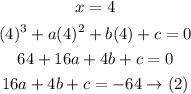
Since when dividing it by x + 2 the remainder is 6

That means when substitute x by -2 the answer will be 6

`\begin{gathered} (-2)^3+a(-2)^2+b(-2)+c=6 \\ -8+4a-2b+c=6 \\ 4a-2b+c=6+8 \\ 4a-2b+c=14\rightarrow(3) \end{gathered}`

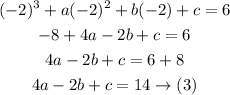
Now, we have a system of equations to solve it to find a, b, c

We will Subtract equation (1) from equation (2) to eliminate c

`\begin{gathered} (16a-a)+(4b--b)+(c-c)=(-64-1) \\ 15a+5b=-65 \\ (15a)/(5)+(5b)/(5)=(-65)/(5) \\ 3a+b=-13\rightarrow(4) \end{gathered}`

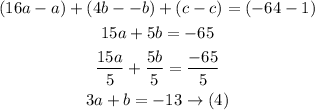
Subtract equation (1) from equation (3) to eliminate c

`\begin{gathered} (4a-a)+(-2b--b)=(14-1) \\ 3a-b=13\rightarrow(5) \end{gathered}`

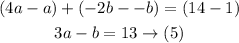
Subtract equation (5) from equation (4) to eliminate a

`\begin{gathered} (3a-3a)+(b--b)=(-13-13) \\ 0+2b=-26 \\ 2b=-26 \\ (2b)/(2)=(-26)/(2) \\ b=-13 \end{gathered}`

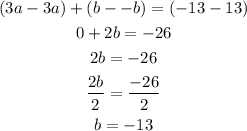
Substitute the value of b in equation (4) to find a

`\begin{gathered} 3a+(-13)=-13 \\ 3a-13+13=-13+13 \\ 3a=0 \\ a=0 \end{gathered}`

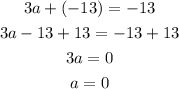
Substitute the values of a and b in equation (1) to find c

`\begin{gathered} 0-(-13)+c=1 \\ 0+13+c=1 \\ 13+c=1 \\ 13-13+c=1-13 \\ c=-12 \end{gathered}`

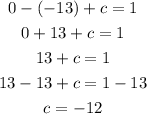
The values of a, b, c are

a = 0

b = -13

c = -12