Question

A study is done on the population of a certain fish species in a lake. Suppose that the population size P(1) after years is given by the following exponentialfunctionP(t) = 420(0.71)^tFind the initial population size.Does the function represent growth or decay?By what percent does the population size change each year?

Answer 1

The population function is given below as

`p(t)=420(0.71)^t`

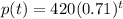
The exponential formula is given blow as

`\begin{gathered} p(t)=ab^t \\ \text{where,} \\ b=1+r(\text{for growth)} \\ b=1-r(\text{for decay)} \end{gathered}`

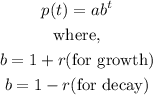
Step 1:

To figure out the initial population size, we will substitute the value of t=0

`\begin{gathered} p(t)=420(0.71)^t \\ p(0)=420(0.71)^0 \\ P(0)=420*1 \\ P(0)=420 \end{gathered}`

Hence,

The initial population size is = 420

Step 2:

To figure out if the function represents growth or decay, we will use the relation below

`\begin{gathered} 1+r<1(\text{decay)} \\ 1+r>1(\text{growth)} \end{gathered}`

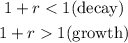
The value of b in the equation is

`b=0.71\text{ <1}`

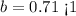
Therefore,

The function in the question represents DECAY

Step 3:

To figure the percentage at which each population size change each year, we will use the formula below

`\%change=\frac{present\text{ population-previous population}}{\text{previous population}}*100\%`

To figure out a present population, we will substitute the value of t to be t=1

`\begin{gathered} p(t)=420(0.71)^t \\ P(1)=420(0.71)^1 \\ P(1)=420*0.71 \\ P(1)=298.2 \end{gathered}`
`\begin{gathered} \%change=\frac{present\text{ population-previous population}}{\text{previous population}}*100\% \\ \%change=(P(0)-P(1))/(P(0))*100\% \\ \%change=(420-298.2)/(420)*100\% \\ \%change=(121.8)/(420)*100\% \\ \%change=29\% \end{gathered}`

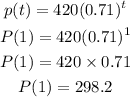
Hence,

The percentage is = 29%