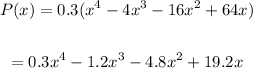Answer:
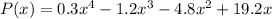
Step-by-step explanation:
Given that the polynomial is of degree 4
Since it has a root of multiplicity 2 at x = 4
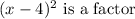
Roots of multiplicity 1 at x = 0
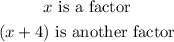
Combining these, we have:
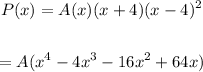
To find the value of A, we use the given point (5, 13.5)
x = 5, P(x) = 13.5
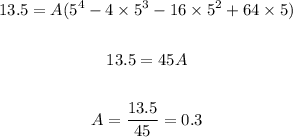
Now, we have: