Question

Which of the following are identities? Check all that apply. O A. sin8 x = 2 sin 4x cos4x O B. sin X + sin5 x = tan3x Cũ= x + CDs5x O c. (sinx-cos ) = 1 + sin 2x 1 O D. 1 - tan2 x 2 tan x

Answer 1

The identity has two equal side

Let us check each one

A)

`\sin 8x=2\sin 4x\cos 4x`

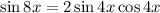
The L.H.S is sin 8x, we will use the rule of the double angle

`\sin 2\theta=2\sin \theta\cos \theta`

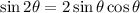
Then divide 8x by 2 and use the rule of the double angle

`\sin 8x=2\sin 4x\cos 4x`

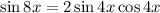
This value = the R.H.S, then

sin 8x = 2sin 4x cos 4x is an identity

Then answer A is an identity

C)

`(\sin x-\cos x)^2=1+2\sin 2x`

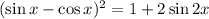
Solve the left side

`\begin{gathered} LHS=(\sin x-\cos x)^2 \\ LHS=\sin ^2x+\cos ^2x-2\sin x\cos x \end{gathered}`

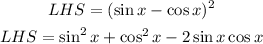
Since sin^2(x) + cos^2(x) = 1, then

`LHS=1-2\sin x\cos x`

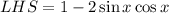
Since 2 sin x cos x = sin(2x), then

`LHS=1-\sin 2x`

But the R.H.S is 1 + sin 2x, then

L.H.S not equal R.H.S

Then answer C is not an identity

D)

`(1-\tan^2x)/(2\tan x)=(1)/(\tan 2x)`

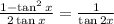
Since tan 2x is equal to

`\tan 2x=(2\tan x)/(1-\tan ^2x)`

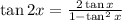
By reciprocal the two sides, then

`(1)/(\tan2x)=(1-\tan ^2x)/(2\tan x)`

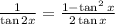
Switch the 2 sides

`(1-\tan^2x)/(2\tan x)=(1)/(\tan 2x)`

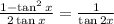
Answer D is an identity

B)

`(\sin x+\sin5x)/(\cos x+\cos5x)=\tan 3x`

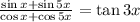
For the left side

`L.H.S=(\sin x+\sin 5x)/(\cos x+\cos 5x)`

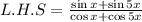
Change angle 5x to 4x + x

`\begin{gathered} \sin 5x=\sin (4x+x) \\ \sin (4x+x)=\sin 4x\cos x+\cos 4x\sin x \end{gathered}`

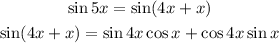
Solve sin4x

`\sin 4x\cos x=(2\sin 2x\cos 2x)(\cos x)=2\cos x\sin 2x\cos 2x`

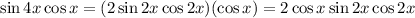
Solve cos4x

`\cos 4x\sin x=(1-2\sin ^22x)(\sin x)=\sin x-2\sin x\sin ^22x`

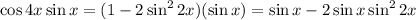
Then sinx+