Question

Calculate the sum of the integers 1 to 100

Answer 1

Given:

Integers from 1 to 100.

Integers are whole numbers that can be positive, negative or zero.

Hence, integers between 1 to 100 are positive whole numbers between 1 and 100.

This is an example of arithmetic sequence increasing by a common difference of 1.

Using the formula for the sum of an arithmetic sequence,

`\begin{gathered} S_n=(n)/(2)(2a+(n-1)d) \\ \text{where;} \\ n\text{ is the number of terms, n = 100} \\ a\text{ is the first term, a = 1} \\ d\text{ is the co}mmon\text{ difference, d = 1} \end{gathered}`

Hence,

`\begin{gathered} S_n=(n)/(2)(2a+(n-1)d) \\ S_(100)=(100)/(2)(2(1)+(100-1))1 \\ S_(100)=50(2+99) \\ S_(100)=50(101) \\ S_(100)=50*101 \\ S_(100)=5050 \end{gathered}`

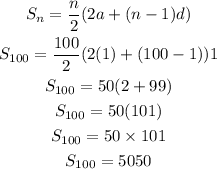
Alternatively using another formula,

`\begin{gathered} S_n=(n)/(2)(a+l) \\ \text{where;} \\ a\text{ is the first term, a = 1} \\ n\text{ is the number of terms, n = 100} \\ l\text{ is the last term, l = 100} \\ \\ S_n=(n)/(2)(a+l) \\ S_(100)=(100)/(2)(1+100) \\ S_(100)=50(101) \\ S_(100)=50*101 \\ S_(100)=5050 \end{gathered}`

Therefore, the sum of the integers from 1 to 100 is 5050.