Question

Write an equation of the line that is perpendicular to y=2x+3 and passes through (-4,3)

Answer 1

Recall the equation of a line with slope m and y-intercept b (in slope-intercept form):

`y=mx+b`

By comparing with the equation y=2x+3, we know that the slope of this line is 2.

For two lines to be perpendicular, their slopes must satisfy the condition:

`m_1\cdot m_2=-1`

Therefore, the slope of any line perpendicular to y=2x+3 must be:

`-(1)/(2)`

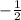
So that (2)(-1/2) = -1 .

Substitute m=-1/2 in the slope-intercept form of the equation of a line:

`y=-(1)/(2)x+b`

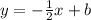
Next, since the line must pass through (-4,3), substitute x=-4 and y=-3 to find the value of b:

`\begin{gathered} 3=-(1)/(2)(-4)+b \\ \Rightarrow3=2+b \\ \Rightarrow b=1 \end{gathered}`

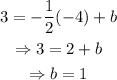
Substitute b=1 in the equation y=(-1/2)x+b:

`y=-(1)/(2)x+1`

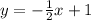
And that is the equation of a line perpendicular to y=2x+3 that passes through (-4,3).