Question

Deion takes 602 milligrams of an antibiotic. Every hour, his body breaks down 30% of the drug. How much will be left after 4 hours?If necessary, round your answer to the nearest tenth.

Answer 1

Exponential Decay

Some quantities undergo exponential decay which means the rate of decrease is proportional to the current quantity.

A mathematical model for exponential decay is:

`P=P_o\cdot(1-r)^t`

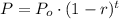
Where:

P: Is the current quantity at time t

Po: Is the initial quantity (at time 0)

r: Is the rate of decay in %

t: Is the time.

The initial quantity of antibiotics is Po = 602 milligrams. The rate of decay is r = 30% = 0.30 per hour. We need to calculate the quantity of antibiotics present after t = 4 hours. Substituting:

`\begin{gathered} P=602\cdot(1-0.3)^4 \\ P=602\cdot(0.7)^4 \\ \text{Calculating:} \\ P=602\cdot0.2401 \\ P=144.5402 \end{gathered}`

Rounding to the nearest tenth:

After 4 hours there will be 144.5 milligrams of antibiotics left