This is an ideal gas problem. We can use the following formula (combined gas law):
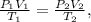
where P represents pressure, V volume, and T temperature. Subindex 1 indicates the initial state and subindex 2 indicates the final state.
We have the following data:
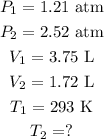
So, we have to clear the final temperature (T2) in the formula of combined gas law and we're going to obtain:
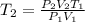
The final step is to replace all the given data:

The answer is that the final temperature would be 280 K.