To solve a system of linear inequalities, we preccend similarly to when we have a system of equations.
We have the two inequalities:
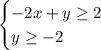
Let's solve the first inequality for y:
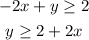
Now, we can graph both equations. To graph the first inequality, we can draw the line y = 2 +2x and shade all the region above that line (because we have y greater or equal than")
To graph a line, we just need to find two points and connect them:
Let's see the value of y for x = 0 and x = 1:

Now we have the points (0, 2) and (1, 4). We can locate them in the cartesian plane and connect them wiht a line:
And since is an inequality, the solutions are the points above the line.
Then we have:
For the second inequality, the border line is y = -2. Is a line parallel to x-axis that passes through y = -2:
And since the inequality is all y bigger or equal to -2, we shade the section above the line:
If we draw the two regions in the same graph we get:
The part the two shades intersect are all the solutions to the system of inequalities.