Given
A rectangle garden has a width of 90 feet. the perimeter is 500 feet.
We are to solve for the length of the garden
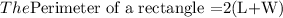
Where L is the length and
W is the width
From the question
W = 90 feet
P = 500 feet
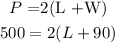
![\begin{gathered} 500=2(L+90) \\ \text{open the bracket} \\ 500=2L+180 \\ \text{collect the like terms} \\ 500-180=2L \\ 320=2L \\ \text{Divide both sides by 2} \\ (320)/(2)=(2l)/(2) \\ \\ L=160\text{ ft} \end{gathered}]()
Another way

The length of the garden is 160 feet