We have the equation:

This is the equation of an ellipse.
We can rearrange the equation to define it explicitly for y as:
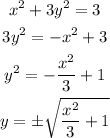
The way the function is defined, we have two values of y for the same value of x.
This is not valid for a function y = f(x), where there has to be one and only one of y for every x in the domain.
Answer: the equation is not a function y = f(x).
NOTE:
For a function y = f(x), x is the input and y is the output.
We can define relationships between inputs and outputs, but functions are a special type of relationships where there is one and only output for each input.
In this case we have inputs (values of x) that have two outputs (values of y), which contradicts the definition of function.