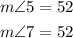1 Answer

Worgon · Answer 1 · 2023-12-12T10:33:40+0000

From the diagram given we notice that angle 2 and angle 4 are vertical opposite angles, which means that the are equal, that is:

$m\angle2=m\angle4$

and hence we have that:

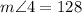
$m\angle4=128$

We also notice that angles 4 and 5 are consecutive interior angles, and since the lines are parallel this means that they have to add to 180°:

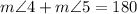
$m\angle4+m\angle5=180$

Plugging the value of angle 4 and solving for angle 5 we have:

$\begin{gathered} 128+m\angle5=180 \\ m\angle5=180-128 \\ m\angle5=52 \end{gathered}$

Finally, we notice that angles 5 and 7 are vertically opposite which means they are equal, hence:

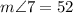
$m\angle7=52$

Therefore, we conclude that:

$\begin{gathered} m\angle5=52 \\ m\angle7=52 \end{gathered}$

Please log in or register to add a comment.