The Rieman sum is used as an approximation when performing integration. It attempts to find an approximate value for the area under the curve.
A left Riemann sum uses rectangles whose top-left vertices are on the curve. A right Riemann sum uses rectangles whose top-right vertices are on the curve. We are therefore given a right-hand Rieman sum.
To calculate the Rieman sum we first note that there are eight rectangles therefore eight intervals.
The base of each rectangle = 0.5
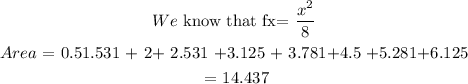
As this is a righ-hand Riemann sum and we can see that the rectangles reach above the cure, we can conclude that it is an over-estimation.