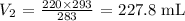Answer:
Step-by-step explanation:
Here, we want to get the volume of the gas at the new temperature
According to Charles' law, the volume of a given mass of gas is directly proportional to the temperature in Kelvin
Mathematically:
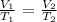
where:
V1 is the initial volume which is 220 mL
T1 is the initial temperature (we convert this to Kelvin by adding 273 : 10 + 273 = 283 K)
V2 is the final volume which is what we want to calculate
T2 is the final temperature which is (20 + 273 = 293 K)
Substituting the values: